4. Depletion¶

In NECP-X, a fine depletion library including 1547 nuclides, and a compressed depletion library including 233 nuclides, are developed for NECP-X. Besides, CRAM is adopted by NECP-X to solve point depletion equations. On the basis of depletion libraries and the point depletion methodology, Predictor-Corrector method with Sub-step method is chosen to couple the transport calculation with the depletion calculation.

4.1. Bateman Equation¶

For each nuclide in the depletion system:

$\frac{d}{{dt}}{N_i}(t) = - \left( {\lambda _i^{{\rm{decay}}} + {\sigma _{{\rm{a,}}i}}\phi } \right) \cdot {N_i}(t) + \sum\limits_j {{b_{j,i}}\lambda _j^{{\rm{decay}}}} \cdot {N_j}(t) + \sum\limits_k {{f_{k,i}}{\sigma _k}\phi } \cdot {N_k}(t)$

where

${\sigma _{{\rm{a,}}i}}$ is the 1-group micro absorption cross section of nuclide i

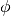$\phi$ is the 1-group neutron scalar flux

${f_{k,i}}$ is the fractions of neutron reactions by nuclide k which lead to the formation of nuclide i；

${b_{j,i}}$ is decay branch ratios of nuclide j which lead to the formation of nuclide i

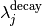$\lambda _j^{{\rm{decay}}}$ is decay constants of nuclide j

The Bateman equations can be presented in a matrix form, which has a formal solution:

$\dot N(t) = A \cdot N(t)$

$N(t) = {e^{tA}} \cdot N(0)$

where

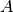is the depletion matrix

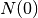is initial atomic density of nuclides

4.2. Chebyshev rational approximation method (CRAM)¶

The eigenvalues of the depletion coefficient matrix A, are clustered around the negative real axis, which can be exploited by making a Chebyshev rational approximation of the exponential function.

${e^{{\rm{ - }}x}} \approx \frac{{{P_k}(x)}}{{{Q_k}(x)}} = {\hat r_{k,k}}(x)$

where

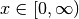
$x \in [0,\infty )$

The resulting rational function can be decomposed into a pole-residue form (partial fraction decomposition) to avoid numerical instability.

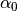${\hat r_{k,k}}(x) = {\alpha _0} + \sum\limits_{i = 1}^k {\frac{{{\alpha _i}}}{{x - {\theta _i}}}}$

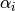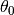where ${\alpha _0}$ is the limiting value of the approximation at infinity, ${\alpha _i}$ and ${\theta _0}$ are the residues and poles

When the denominator and numerator orders of the Chebyshev approximation are selected equal and even, the poles form conjugate pairs and the imaginary parts cancel out for a real valued variable.

${\hat r_{k,k}}(x) = {\alpha _0} + \sum\limits_{i = 1}^k {\frac{{{\alpha _i}}}{{x - {\theta _i}}}} = {\alpha _0} + 2Re\sum\limits_{i = 1}^{k/2} {\frac{{{\alpha _i}}}{{x - {\theta _i}}}}$

When this approximation is applied to the matrix exponential,the depletion equation with matrix form can be presented as the following form:

$\overrightarrow N (x) = {\alpha _0}\overrightarrow N (0) + 2\left[ {Re\sum\limits_{i = 1}^{k/2} {{\alpha _i}{{(At + \;{\theta _i}I)}^{ - 1}}} } \right]\overrightarrow N (0)$

Due to the special structure of the depletion matrix, this can be accurately and efficiently solved by using symbolic LU decomposition and Gaussian elimination.

CRAM accuracy of different orders

depletion matrix structure

4.3. The coupling scheme¶

4.3.1. The predictor-corrector method¶

The predictor-corrector method cancel out the errors in atomic densities by averaging the begin of step (BOS) and end of step (EOS) reaction rates.

${N_{t2}}{\rm{ = }}\frac{{N_{{\rm{t}}2}^P({R_{t1}}){\rm{ + }}N_{t2}^C(R_{t2}^P)}}{2}$

where

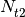$N_{t2}^{}$ is particle number density at t2

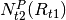$N_{t2}^P({R_{t1}})$ is predicted particle number density at t2

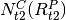$N_{t2}^C(R_{t2}^P)$ is corrected particle number density at t2

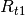${R_{t1}}$ is the 1-group micro reaction rates at t1

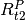$R_{t2}^P$ is predicted 1-group micro reaction rates at t2

4.3.2. The sub-step method¶

The sub-step method is applied to perform multiple depletion calculations between successive transport calculations, allowing reaction rates to be various piecewise constant rather than only one constant. The nth flux belonging to the nth sub-step represents the flux at time t1+nΔt/N. It is used by the depletion calculations as:

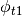${\phi _n}{\rm{ = }}{\phi _{t1}}{f_{n - 1}}$

${f_{n - 1}}{\rm{ = }}\frac{{{P_{t1}}}}{{\sum\limits_j {\sum\limits_i {N_{n - 1}^{i,j}{\kappa _i}\sigma _{t1}^{f,i,j}\phi _{n - 1}^j{V_j}} } }}$

where ${\phi _{t1}}$ is unnormalized 1-group scalar flux at t1

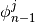$\phi _{n - 1}^j$ is the 1-group scalar flux at time t1+nΔt/N for region j

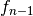${f_{n - 1}}$ is power normalized factor

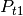${P_{t1}}$ is the total power at t1

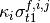${\rm{ }}{\kappa _i}\sigma _{t1}^{f,i,j}$ is the energy per fission multiplied by the microscopic fission cross section of region j and nuclide i at t1

${\rm{ }}N_{n - 1}^{i,j}$ is the nuclide concentration of n-1 sub-step

【Close Window】