2. Resonance¶
NECP-X uses a pseudo-resonant-nuclide subgroup method (PRNSM) which is proposed
by NECP lab in Xi’an Jiaotong University. There are six parts in this section.
Firstly, the equivalence procedure of 1-D cylindrical problem will be described.
Secondly, the neutron slowing-down equation will be simplified.
Thirdly, the pseudo resonant nuclide will be defined. The afterward derivations
are based on the 1-D cylindrical problem. Fourthly, the theory of physical
probability table based on IR approximation for the pseudo resonant nuclide will be
derived. Fifthly,the Subgroup Fixed Source Problem (SFSP) consistent with the
physical probability table will be formulated. Finally, the Super Homogenization
(SPH) correction for effective self-shielded XS is described.
2.1. The Equivalent 1-D Cylindrical Problem¶
The Dancoff correction factor of the target fuel pin is defined as:
(1)¶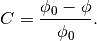
where  is the flux of the target fuel pin in the isolated system;
is the flux of the target fuel pin in the isolated system;
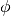 is the flux of the target fuel pin in the lattice system.
The calculation flow of the neutron current method is as follows.
is the flux of the target fuel pin in the lattice system.
The calculation flow of the neutron current method is as follows.
Firstly, Equation (2) is solved in the space domain of the lattice system and the flux of the target fuel pin in the lattice system is obtained by:
(2)¶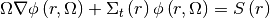
where 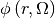 is the angular flux;
is the angular flux;
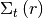 is the total XS;
is the total XS;  is the fixed neutron source. For the fuel regions, the black body assumption is
adopted. The total XS is set to be sufficiently large,
is the fixed neutron source. For the fuel regions, the black body assumption is
adopted. The total XS is set to be sufficiently large, 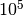 cm-1 for example,
and the scattering XS is assumed to be zero. The fixed neutron source is set to
be zero. For the moderator regions, the total XS is set to be equal to be value
of the potential scattering XS and The scattering XS is set to be zero. The
intensities of fixed neutron source are set to be equal to the value of the
potential scattering XS. Secondly, Equation (2) is solved in the space
domain of the isolated system of the target fuel pin and
cm-1 for example,
and the scattering XS is assumed to be zero. The fixed neutron source is set to
be zero. For the moderator regions, the total XS is set to be equal to be value
of the potential scattering XS and The scattering XS is set to be zero. The
intensities of fixed neutron source are set to be equal to the value of the
potential scattering XS. Secondly, Equation (2) is solved in the space
domain of the isolated system of the target fuel pin and  is obtained.
The same assumptions as used in the first step are adopted for the fuel regions
and moderator regions. Finally, the Dancoff correction factor is the target fuel
pin is evaluated according to Equation (1).
Assume that there exists a 1-D cylindrical pin whose Dancoff correction factor
is equivalent to that of the target fuel pin. The Dancoff correction factor can
also be obtained by collision probability:
is obtained.
The same assumptions as used in the first step are adopted for the fuel regions
and moderator regions. Finally, the Dancoff correction factor is the target fuel
pin is evaluated according to Equation (1).
Assume that there exists a 1-D cylindrical pin whose Dancoff correction factor
is equivalent to that of the target fuel pin. The Dancoff correction factor can
also be obtained by collision probability:
(3)¶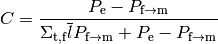
where 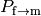 is the collision probability from the
fuel region to the moderator region in the 1-D cylindrical system;
is the collision probability from the
fuel region to the moderator region in the 1-D cylindrical system;  is the escape probability from the fuel;
is the escape probability from the fuel; 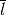 is the average chord
length of the fuel pin;
is the average chord
length of the fuel pin; 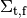 is the total XS of the fuel region.
is the total XS of the fuel region.
 ,
, 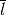 and
and 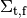 are
independent of the outer radius of the 1-D cylindrical pin, but :math:’P_{{rm{f}} to {rm{m}}}’
is a function of the outer radius. Therefore Equation (3) can be rewritten as:
are
independent of the outer radius of the 1-D cylindrical pin, but :math:’P_{{rm{f}} to {rm{m}}}’
is a function of the outer radius. Therefore Equation (3) can be rewritten as:
(4)¶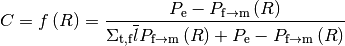
where 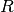 is the outer radius of the 1-D cylindrical pin. As the Dancoff
correction factor is known, the outer radius can be obtained by binary search.
The diagram for this equivalence procedure is shown below.
is the outer radius of the 1-D cylindrical pin. As the Dancoff
correction factor is known, the outer radius can be obtained by binary search.
The diagram for this equivalence procedure is shown below.
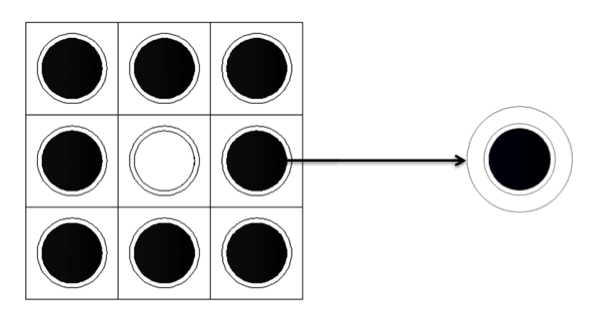
Equivalence between a fuel pin cell in lattice and a 1-D cylindrical fuel pin cell
2.2. Simplification of the neutron slowing-down equation¶
The neutron slowing down equation can be written as:
(5)¶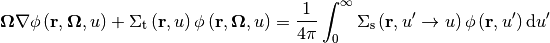
Under the IR approximation, Equation (5) can be rewritten as:
(6)¶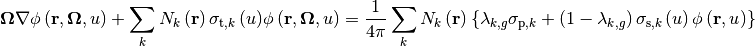
where 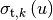 is the energy-dependent microscopic total XS.
is the energy-dependent microscopic total XS.
2.3. Definition of the pseudo resonant nuclide¶
Define a pseudo background nuclide whose atomic weight ratio and potential
scattering XS is identical to that of 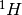 . There is no absorption
for the pseudo background nuclide. Then define a pseudo resonant nuclide whose
energy-dependent XS is averaged by number densities of all the resonant nuclides.
The number density of the pseudo resonant nuclide in the equivalent 1-D problem is:
. There is no absorption
for the pseudo background nuclide. Then define a pseudo resonant nuclide whose
energy-dependent XS is averaged by number densities of all the resonant nuclides.
The number density of the pseudo resonant nuclide in the equivalent 1-D problem is:
(7)¶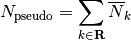
where 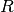 is the assemblage of resonant nuclides;
is the assemblage of resonant nuclides; 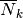 is the volume averaged number density for resonant nuclide in fuel region.
In the afterward derivation, the volume averaged number density will be assumed
for all the resonant nuclides in fuel regions.
For an infinite homogeneous system mixed by several resonant nuclides and the pseudo background nuclide, the solution of Equation (6) can be written as:
is the volume averaged number density for resonant nuclide in fuel region.
In the afterward derivation, the volume averaged number density will be assumed
for all the resonant nuclides in fuel regions.
For an infinite homogeneous system mixed by several resonant nuclides and the pseudo background nuclide, the solution of Equation (6) can be written as:
(8)¶![\phi \left( u \right) &= \frac{{\sum\limits_k {{N_k}{\lambda _{k,g}}{\sigma _{{\rm{p}},k}}} }}{{\sum\limits_k {{N_k}\left[ {{\sigma _{{\rm{a}},k}}\left( u \right) + {\lambda _{k,g}}{\sigma _{{\rm{s}},k}}\left( u \right)} \right]} }}&= \frac{{{{\left( {\lambda {\sigma _{\rm{p}}}} \right)}_{{\rm{pseudo}},g}} + {\sigma _0}}}{{{\sigma _{{\rm{a,pseudo}}}}\left( u \right) + \left[ {{\sigma _{{\rm{s}},{\rm{pseudo}}}}\left( u \right) - {{\left( {\lambda {\sigma _{\rm{p}}}} \right)}_{{\rm{pseudo}},g}}} \right] + {{\left( {\lambda {\sigma _{\rm{p}}}} \right)}_{{\rm{pseudo}},g}} + {\sigma _0}}}&= \frac{{{\sigma _{\rm{b}}}}}{{{\sigma _{{\rm{inter,pseudo}}}}\left( u \right) + {\sigma _{\rm{b}}}}}](/__local/B/BA/C6/72EBFD332F4FBABBF30D649FBA0_3169AA4D_C97.png)
2.4. Physical probability table for the pseudo resonant nuclide¶
The XS of pseudo resonance nuclide can be written as:
(9)¶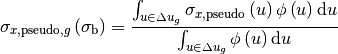
Apply Equation (8) to equation (9) ,then we can get:
(10)¶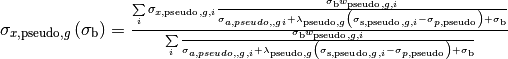
where 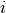 is subgroup index;
is subgroup index; 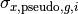 is subgroup intermediate XS;
is subgroup intermediate XS; 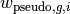 is subgroup weight.
When get the subgroup parameters, translate muti-group xs to discrete subgroup form
for each resonance nuclide:
is subgroup weight.
When get the subgroup parameters, translate muti-group xs to discrete subgroup form
for each resonance nuclide:
(11)¶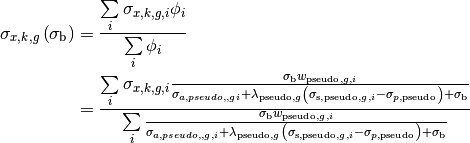
where 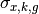 is the subgroup XS of nuclide
is the subgroup XS of nuclide 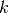 in
in 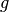 group and
group and 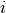 subgroup which is calculated by least square fit with
subgroup which is calculated by least square fit with 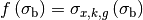 .
.
2.5. SFSP for the pseudo resonant nuclide¶
Since there is only one resonance nuclide in the problem, i.e. pseudo resonant nuclide,
the Subgroup Fixed Source Problem(SFSP) of resonant nuclide can be obtained by integrating
Equation sd-eq1`on subgroup :math:`i :
(12)¶![\begin{array}{l}{\bf{\Omega }}\nabla {\phi _{g,i}}\left( {{\bf{r}},{\bf{\Omega }}} \right) + \left[ {{{\overline N }_{{\rm{pseudo}}}}{\sigma _{{\rm{t}},pseudo,g,i}} + \sum\limits_{k \notin {\bf{R}}} {{N_k}\left( {\bf{r}} \right){\sigma _{t,k,g}}} } \right]{\phi _{g,i}}\left( {{\bf{r}},{\bf{\Omega }}} \right) = \\\frac{1}{{4\pi }}{w_{{\rm{pseudo}},g,i}}\left\{ \begin{array}{l}{\overline N _{{\rm{pseudo}}}}\left[ {{\lambda _{{\rm{pseudo}}.g}}{\sigma _{{\rm{p}},{\rm{pseudo}}}} + \left( {1 - {\lambda _{{\rm{pseudo}},g}}} \right){\sigma _{{\rm{s}},{\rm{pseudo}},g,i}}{\phi _{g,i}}\left( {\bf{r}} \right)} \right] + \\\sum\limits_{k \notin {\bf{R}}} {{N_k}\left( {\bf{r}} \right)\left[ {{\lambda _{k,g}}{\sigma _{{\rm{p}},k}} + \left( {1 - {\lambda _{k,g}}} \right){\sigma _{{\rm{s}},k,g}}{\phi _{g,i}}\left( {\bf{r}} \right)} \right]}\end{array} \right\}\end{array}](/__local/8/E9/D3/3D96D8CB2C5879C05DC30E81A76_C01B5AC8_1007.png)
where 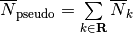 is the average nuclide density;
is the average nuclide density; 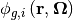 is the subgroup angular flux;
is the subgroup angular flux; 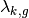 is the average Goldstein-Cohen Factor of nuclide
is the average Goldstein-Cohen Factor of nuclide 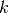 in group
in group 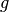 .
By solving Equation (12) and get the subgroup scalar flux, effective self-shielded XS can be obtained by
Equation (13):
.
By solving Equation (12) and get the subgroup scalar flux, effective self-shielded XS can be obtained by
Equation (13):
(13)¶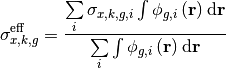
2.6. SPH correction for effective self-shielded XS¶
The effective self-shielded XS is defined as:
(14)¶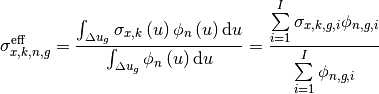
However, utilization of the effective self-shielded XS directly in afterward multi-group transport calculation cannot preserve the reaction rate. Therefore, the SPH correction factor is multiplied to the effective self-shielded XS:
(15)¶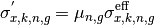
The SPH correction factor is computed in following procedures:
1) Set 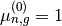 at the first step or use the SPH correction factor obtained in the last iteration, solve for the linear system:
at the first step or use the SPH correction factor obtained in the last iteration, solve for the linear system:
(16)¶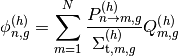
- Normalize the flux by preserving average flux in the moderator regions;
- Compute the SPH correction factor by:
(17)¶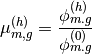
- Repeat step 1) to step 3) until the SPH correction factors converge.