3. Transport¶

In NECP-X, 2D/1D transport method is used including 2DMOC radially and 1DSN axially. In NECP-X, Jacobi iteration strategy is used to improve efficiency and stability. Multi-level Parallel method is used in NECP-X and has been tested on 16000CPUs. The C5G7 benchmark and the VERA benchmark have been performed to verify the accuracy of NECP-X.

3.1. 2D/1D transport method¶

The original 3D multi-group transport equation can be written as:

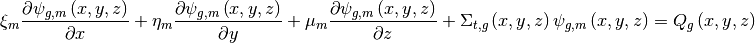
${\xi _m}\frac{{\partial {\psi _{g,m}}\left( {x,y,z} \right)}}{{\partial x}} + {\eta _m}\frac{{\partial {\psi _{g,m}}\left( {x,y,z} \right)}}{{\partial y}} + {\mu _m}\frac{{\partial {\psi _{g,m}}\left( {x,y,z} \right)}}{{\partial z}} + {\Sigma _{t,g}}\left( {x,y,z} \right){\psi _{g,m}}\left( {x,y,z} \right) = {Q_g}\left( {x,y,z} \right)$

The radial 2D equation is obtained by integrating over axial direction in plane L:

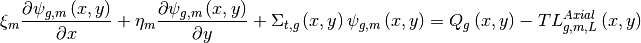
${\xi _m}\frac{{\partial {\psi _{g,m}}\left( {x,y} \right)}}{{\partial x}} + {\eta _m}\frac{{\partial {\psi _{g,m}}\left( {x,y} \right)}}{{\partial y}} + {\Sigma _{t,g}}\left( {x,y} \right){\psi _{g,m}}\left( {x,y} \right) = {Q_g}\left( {x,y} \right) - TL_{g,m,L}^{Axial}\left( {x,y} \right)$

where:

$TL_{g,m,L}^{Axial}\left( {x,y} \right) = \frac{{{\mu _m}}}{{\Delta {z_k}}}\left[ {{\psi _{g,m,L + 1/2}}\left( {x,y} \right) - {\psi _{g,m,L - 1/2}}\left( {x,y} \right)} \right]$

The axial 1D equation is obtained by integrate Eq.(1) over radial direction in pin p:

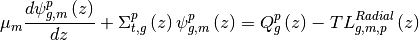
${\mu _m}\frac{{d\psi _{g,m}^p\left( z \right)}}{{dz}} + \Sigma _{t,g}^p\left( z \right)\psi _{g,m}^p\left( z \right) = Q_g^p\left( z \right) - TL_{g,m,p}^{Radial}\left( z \right)$

where:

$TL_{g,m,p}^{Radial}\left( z \right) = \frac{{{\xi _m}}}{{\Delta x}}\left[ {\psi _{g,m,x + }^p\left( z \right) - \psi _{g,m,x - }^p\left( z \right)} \right] + \frac{{{\eta _m}}}{{\Delta y}}\left[ {\psi _{g,m,y + }^p\left( z \right) - \psi _{g,m,y - }^p\left( z \right)} \right]$

In NECP-X, the SN diamond difference method is applied in the 1D calculation and anisotropic leakage term is used in 2D/1D transport calculation. Iteration between the 2D MOC and 1D SN calculations are performed until both the eigenvalue and fission rate are converged.

3.2. Jacobi iteration strategy¶

The Jacobi iteration strategy is:

Update fission source and leakage items.

Convergence judgement

Update the scattering source for all energy groups

MOC sweeping for all energy groups

End convergence judgement

The Gauss-Seidel iteration strategy is:

Update fission source and leakage items.

Energy group sweeping loop (from high energy to low)

Convergence judgement

Update the scattering source for the energy group

MOC sweeping

End convergence judgement

End energy group loop

It is the 2D MOC sweeping module that consumes most of time in 2D/1D transport method. Therefore it is privileged to improve the efficiency of MOC sweeping module. The advantage of the group-sweeping-inside strategy lies in its high efficiency, as flux calculation can be carried out for all energy groups at the same time. Compared to group-sweeping-outside strategy, more cache is used and addressing in memory time is less.

Flowchart of NECP-X 2D/1D solver is shown as below:

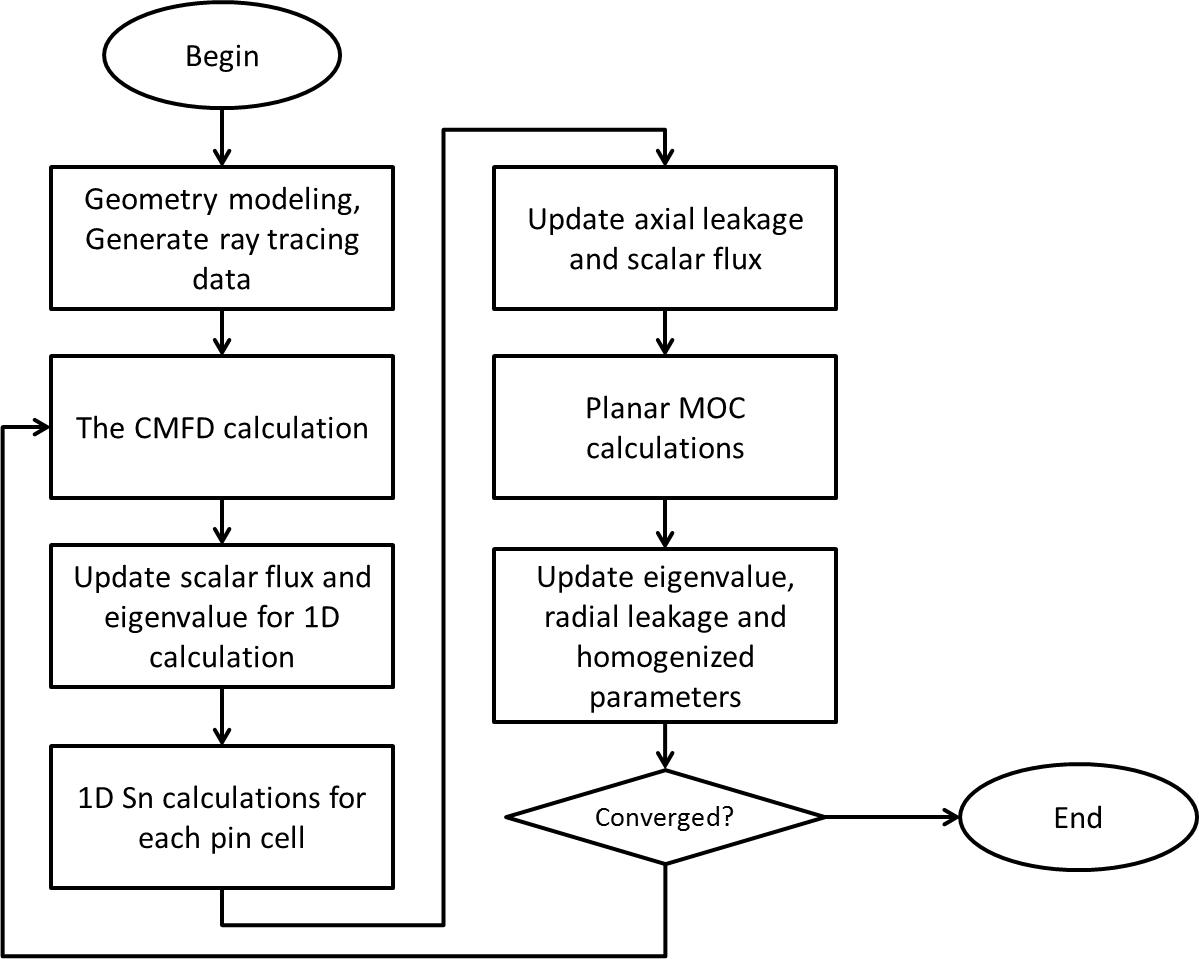
Flow chart of the 2D/1D transport method

3.3. CMFD solver with PETSc math library¶

Coarse Mesh Finite Difference(CMFD) has been verified to be an effective way of accelerating high order 2D/1D transport calculation. It is implemented in NECP-X and odCMFD is used to make the CMFD acceleration more stable.

PETSc is a math library to solve partial differential equation. Free-matrix format solver is supported by PETSc, which avoids generating the huge matrix. Matrix-multiply-vector algorithm needs to be provided by PETSc users and iteration process is executed automatically by PETSc.

In NECP-X, there are two CMFD solvers. One is based on the GMRES algorithm with constructing matrix explicitly and nonzero storage technology. Another one is based on GMRES algorithm with free-matrix format in PETSc. The solver based on PETSc is used as default because of parallel ability.

Parallel efficiency issues for the CMFD solver based on PETSc is solved by using domain decomposition and Gauss-Seidel iteration to decrease the size of matrix.

3.4. Multi-level parallel method¶

With the development of computer technology, parallel computing has become a universal acceleration method. As for the direct whole-core transport calculation, efficiency and memory become far beyond a personal computer. Multi-level parallel capability is necessary, which is implemented in NECP-X, including space, angular and ray parallels. Figure below shows the multi-level parallel strategy in NECP-X. The massively parallel ability has been verified on 16000 CPUs and parallel efficiency of NECP-X are still being tested on Tianhe-2, which is top 2 supercomputer in the world.

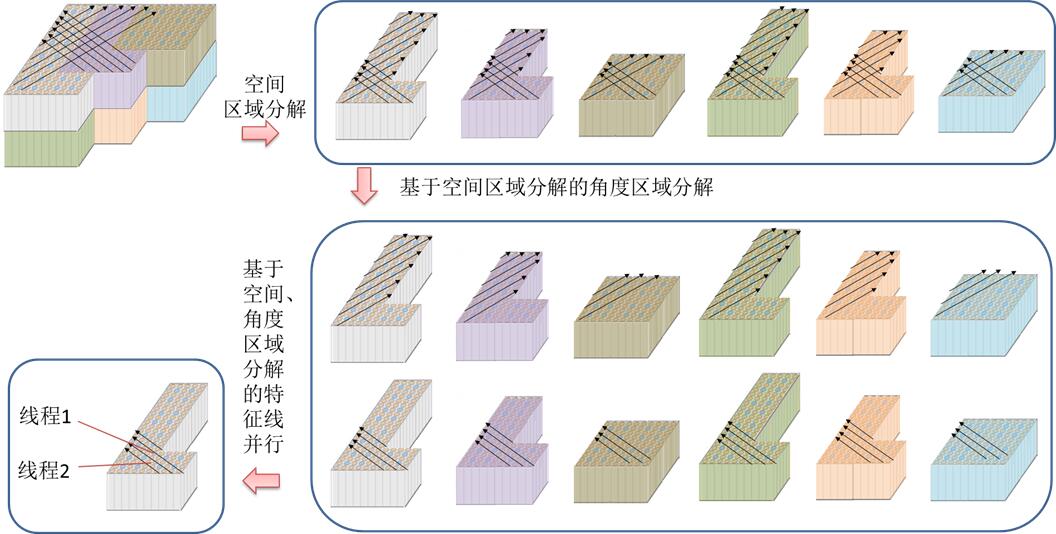
multi-level parallel strategy in NECP-X