5. Transient¶

There are two transient methods in NECP-X, which are flully implicit method(FIM) and predictor-corrector quasi-static method(PCQS). For transient calculation, a 3D transient fixed source problem(TFSP) is obtained by discreting the time-dependent variable. And 2D/1D TFSP is the replacement of the direct 3D heterogeous TFSP. And 3D CMFD TFSP is used to accelerate the convergence of 2D/1D TFSP. For PCQS, the CMFD adjoint flux is used as weight function to get point kinetics parameters.

5.1. 3D TFSP¶

Fully implicit method is used for time-dependent variable and isotropic assumption for the time derivative term is introduced as follows shown:

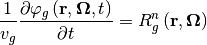
$\frac{1}{{{v_g}}}\frac{{\partial {\varphi _g}\left( {{\bf{r}},{\bf{\Omega }},t} \right)}}{{\partial t}} = R_g^n\left( {{\bf{r}},{\bf{\Omega }}} \right)$

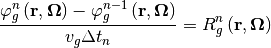
$\frac{{\varphi _g^n\left( {{\bf{r}},{\bf{\Omega }}} \right) - \varphi _g^{n - 1}\left( {{\bf{r}},{\bf{\Omega }}} \right)}}{{{v_g}\Delta {t_n}}} = R_g^n\left( {{\bf{r}},{\bf{\Omega }}} \right)$

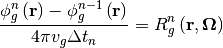
$\frac{{\phi _g^n\left( {\bf{r}} \right) - \phi _g^{n - 1}\left( {\bf{r}} \right)}}{{4\pi {v_g}\Delta {t_n}}} = R_g^n\left( {{\bf{r}},{\bf{\Omega }}} \right)$

And 2nd order precursor integration technique for precursor term is used as follows:

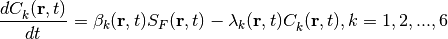
$\frac{{dC_k^{}({\bf{r}},t)}}{{dt}} = {\beta _k}({\bf{r}},t){S_F}({\bf{r}},t) - {\lambda _k}({\bf{r}},t)C_k^{}({\bf{r}},t),k = 1,2,...,6$

So the final form of 3D TFSP is obained as follows:

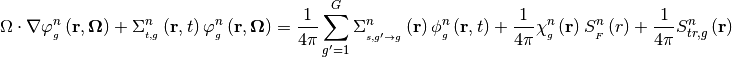
$\Omega \cdot \nabla \varphi _{_g}^n\left( {{\bf{r}},{\bf{\Omega }}} \right) + \Sigma _{_{t,g}}^n\left( {{\bf{r}},t} \right)\varphi _{_g}^n\left( {{\bf{r}},{\bf{\Omega }}} \right) = \frac{1}{{4\pi }}\sum\limits_{g' = 1}^G {\Sigma _{_{s,g' \to g}}^n\left( {\bf{r}} \right)\phi _{_g}^n\left( {{\bf{r}},t} \right)} + \frac{1}{{4\pi }}\chi _{_g}^n\left( {\bf{r}} \right)S_{_F}^n\left( r \right) + \frac{1}{{4\pi }}S_{tr,g}^n\left( {\bf{r}} \right)$

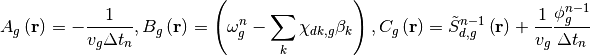
${A_g}\left( {\bf{r}} \right) = - \frac{1}{{{v_g}\Delta {t_n}}},{B_g}\left( {\bf{r}} \right) = \left( {\omega _g^n - \sum\limits_k {{\chi _{dk,g}}{\beta _k}} } \right),{C_g}\left( {\bf{r}} \right) = \tilde S_{d,g}^{n - 1}\left( {\bf{r}} \right) + \frac{1}{{{v_g}}}\frac{{\phi _g^{n - 1}}}{{\Delta {t_n}}}$

5.2. 2D/1D TFSP¶

5.2.1. 2D TFSP¶

To obtain the 2D transient fixed source problem, you need to integrate the 3D TFSP over z direction for each plane and discrete it over angle m, then you need to define axial integrated flux, cross section and transient source as follows:

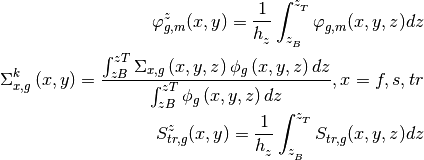
$\varphi _{g,m}^z(x,y) = \frac{1}{{h_z^{}}}\int_{z_B^{}}^{z_T^{}} {\varphi _{g,m}^{}(x,y,z)dz} \\\Sigma _{x,g}^k\left( {x,y} \right) = \frac{{\int_{zB}^{zT} {{\Sigma _{x,g}}\left( {x,y,z} \right){\phi _g}\left( {x,y,z} \right)dz} }}{{\int_{zB}^{zT} {{\phi _g}\left( {x,y,z} \right)dz} }},x = f,s,tr\\S_{tr,g}^z(x,y) = \frac{1}{{h_z^{}}}\int_{z_B^{}}^{z_T^{}} {S_{tr,g}^{}(x,y,z)dz}$

So you will get the final form for 2D transport TFSP as follows:

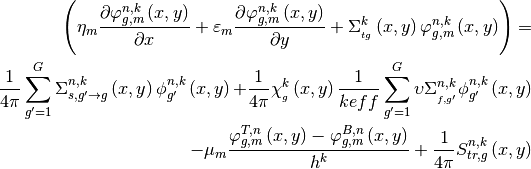
$\left( {{\eta _m}\frac{{\partial \varphi _{g,m}^{n,k}\left( {x,y} \right)}}{{\partial x}} + {\varepsilon _m}\frac{{\partial \varphi _{g,m}^{n,k}\left( {x,y} \right)}}{{\partial y}} + \Sigma _{_{tg}}^k\left( {x,y} \right)\varphi _{g,m}^{n,k}\left( {x,y} \right)} \right) = \\\frac{1}{{4\pi }}\sum\limits_{g' = 1}^G {\Sigma _{s,g' \to g}^{n,k}\left( {x,y} \right)\phi _{g'}^{n,k}\left( {x,y} \right) + } \frac{1}{{4\pi }}\chi _{_g}^k\left( {x,y} \right)\frac{1}{{keff}}\sum\limits_{g' = 1}^G {\upsilon \Sigma _{_{f,g'}}^{n,k}} \phi _{g'}^{n,k}\left( {x,y} \right)\\- {\mu _m}\frac{{\varphi _{g,m}^{T,n}\left( {x,y} \right) - \varphi _{g,m}^{B,n}\left( {x,y} \right)}}{{{h^k}}} + \frac{1}{{4\pi }}S_{tr,g}^{n,k}\left( {x,y} \right)$

And the above equation can be solved by 2D MOC solver by adding an extra transient source term.

5.2.2. 1D TFSP¶

To obtain the 1D transient fixed source problem, you need to integrate the 3D TFSP over x-y direction for each coarse mesh cell and discrete it over angle m, then you need to define axially integrated flux, cross section and transient source as follows:

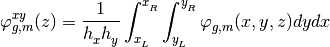
$\varphi _{g,m}^{xy}(z) = \frac{1}{{h_x^{}h_y^{}}}\int_{x_L^{}}^{x_R^{}} {\int_{y_L^{}}^{y_R^{}} {\varphi _{g,m}^{}(x,y,z)dydx} }$

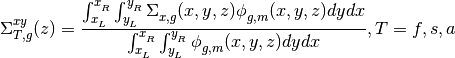
$\Sigma _{T,g}^{xy}(z) = \frac{{\int_{x_L^{}}^{x_R^{}} {\int_{y_L^{}}^{y_R^{}} {\Sigma _{x,g}^{}(x,y,z)\phi _{g,m}^{}(x,y,z)dydx} } }}{{\int_{x_L^{}}^{x_R^{}} {\int_{y_L^{}}^{y_R^{}} {\phi _{g,m}^{}(x,y,z)dydx} } }},T = f,s,a$

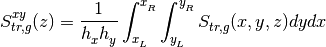
$S_{tr,g}^{xy}(z) = \frac{1}{{h_x^{}h_y^{}}}\int_{x_L^{}}^{x_R^{}} {\int_{y_L^{}}^{y_R^{}} {S_{tr,g}^{}(x,y,z)dydx} }$

So you will get the final form for 1D transport TFSP as follows:

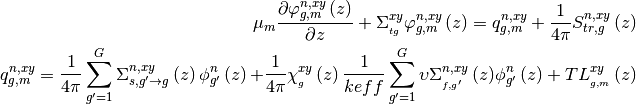
${\mu _m}\frac{{\partial \varphi _{g,m}^{n,xy}\left( z \right)}}{{\partial z}} + \Sigma _{_{tg}}^{xy}\varphi _{g,m}^{n,xy}\left( z \right) = q_{g,m}^{n,xy} + \frac{1}{{4\pi }}S_{tr,g}^{n,xy}\left( z \right)\\q_{g,m}^{n,xy} = \frac{1}{{4\pi }}\sum\limits_{g' = 1}^G {\Sigma _{s,g' \to g}^{n,xy}\left( z \right)\phi _{g'}^n\left( z \right) + } \frac{1}{{4\pi }}\chi _{_g}^{xy}\left( z \right)\frac{1}{{keff}}\sum\limits_{g' = 1}^G {\upsilon \Sigma _{_{f,g'}}^{n,xy}\left( z \right)} \phi _{g'}^n\left( z \right) + TL_{_{g,m}}^{xy}\left( z \right)$

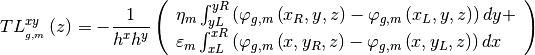
$TL_{_{g,m}}^{xy}\left( z \right) = - \frac{1}{{{h^x}{h^y}}}\left( \begin{array}{l}{\eta _m}\int_{yL}^{yR} {\left( {{\varphi _{g,m}}\left( {{x_R},y,z} \right) - {\varphi _{g,m}}\left( {{x_L},y,z} \right)} \right)dy} + \\{\varepsilon _m}\int_{xL}^{xR} {\left( {{\varphi _{g,m}}\left( {x,{y_R},z} \right) - {\varphi _{g,m}}\left( {x,{y_L},z} \right)} \right)dx}\end{array} \right)$

And the above equation can be solved by 1D Sn solver by adding an extra transient source term.

5.3. CMFD TFSP¶

The 3D CMFD TFSP is used to accelerate the convergence of 2D/1D. And 3D CMFD TFSP is solved by sweeping method.

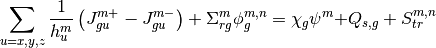
$\sum\limits_{u = x,y,z} {\frac{1}{{h_u^m}}\left( {J_{gu}^{m + } - J_{gu}^{m - }} \right)} + \Sigma _{rg}^m\phi _g^{m,n} = {\chi _g}{\psi ^m}{\rm{ + }}{Q_{s,g}} + S_{tr}^{m,n}$

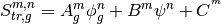
$S_{tr,g}^{m,n} = A_g^m\phi _g^n + {B^m}{\psi ^n} + {C^{^m}}$

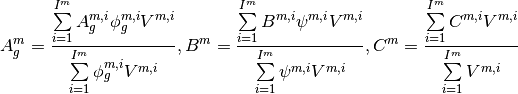
$A_g^m = \frac{{\sum\limits_{i = 1}^{{I^m}} {A_g^{m,i}\phi _g^{m,i}{V^{m,i}}} }}{{\sum\limits_{i = 1}^{{I^m}} {\phi _g^{m,i}{V^{m,i}}} }},B_{}^m = \frac{{\sum\limits_{i = 1}^{{I^m}} {B_{}^{m,i}\psi _{}^{m,i}{V^{m,i}}} }}{{\sum\limits_{i = 1}^{{I^m}} {\psi _{}^{m,i}{V^{m,i}}} }},C_{}^m = \frac{{\sum\limits_{i = 1}^{{I^m}} {C_{}^{m,i}{V^{m,i}}} }}{{\sum\limits_{i = 1}^{{I^m}} {{V^{m,i}}} }}$

5.4. PCQS¶

To reduce calculation time, PCQS method is introduced in NECP-X. PCQS can ensure the calculation precision with relatively large time step to reduce calculation burden. For PCQS, predictor calculation is carried out by solving a 3D TFSP with relatively large time step, and corrector calculation is carried out by solving point kinetics equations with relatively small time step.

The splitting factor is used in neutron flux as follows:

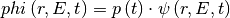
$phi \left( {r,E,t} \right) = p\left( t \right) \cdot \psi \left( {r,E,t} \right)$

To ensure the splitting unique, a constraint condition is used as follows:

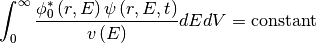
${\int_0^\infty {\frac{{\phi _0^*\left( {r,E} \right)\psi \left( {r,E,t} \right)}}{{v\left( E \right)}}dEdV} } = {\rm{constant}}$

Finally a point kinetics equation set is obtained as follows:

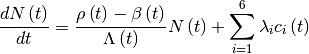
$\frac{{dN\left( t \right)}}{{dt}} = \frac{{\rho \left( t \right) - \beta \left( t \right)}}{{\Lambda \left( t \right)}}N\left( t \right) + \sum\limits_{i = 1}^6 {{\lambda _i}{c_i}\left( t \right)}$

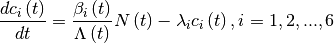
$\frac{{d{c_i}\left( t \right)}}{{dt}} = \frac{{{\beta _i}\left( t \right)}}{{\Lambda \left( t \right)}}N\left( t \right) - {\lambda _i}{c_i}\left( t \right),i = 1,2,...,6$

And the point kinetics parameters are shown as follows:

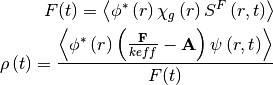
$F(t) = \left\langle {{\phi ^*}\left( r \right){\chi _g}\left( r \right){S^F}\left( {r,t} \right)} \right\rangle \\\rho \left( t \right) = \frac{{\left\langle {{\phi ^*}\left( r \right)\left( {\frac{{\bf{F}}}{{keff}} - {\bf{A}}} \right)\psi \left( {r,t} \right)} \right\rangle }}{{F(t)}}$

And the PCQS scheme is shown in below:

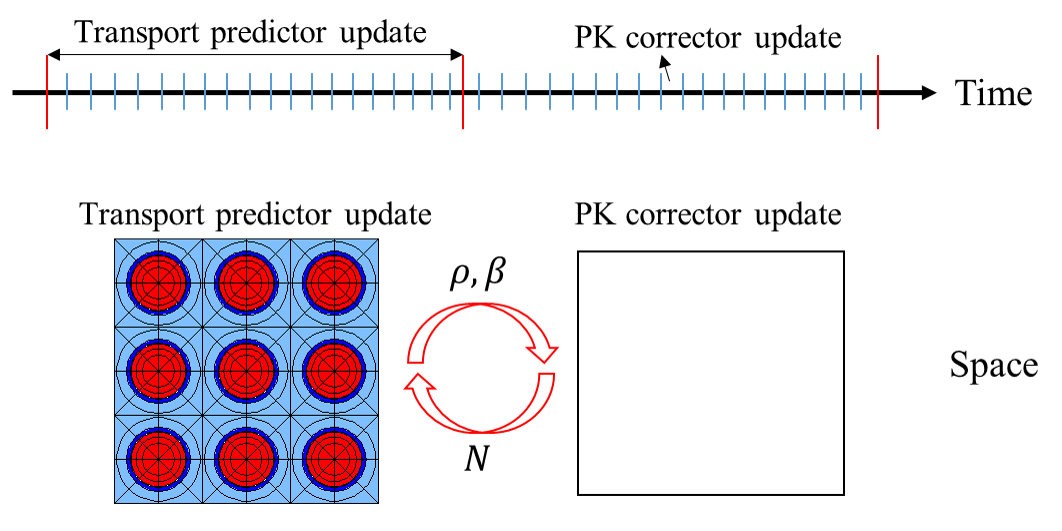
The scheme of the PCQS method