6. T/H coupling¶

The nonlinear relationship between different physical quantities associated with neutronics and thermal-hydraulics has been a challenging problem in coupling these two codes. Several numerical solution strategies have been investigated, such as Newton method, fixed point iteration, JFNK, etc. Fixed point iteration, which is the simplest and perhaps most common approach, is used in NECP-X. This strategy is performed by sequentially solving NECP-X and SUSBC independently within a global iteration loop. The following parts focus on another two key issues, i.e., coupling method and spatial mapping.

6.1. Coupling method

Generally, there are two methods for coupling two separate codes into one integrated system: external coupling and internal coupling. For the external coupling method, the transfer of coupling parameters is usually realized through external files. Also an extra coupling script is needed to execute the coupling calculation. This coupling approach is flexible and simple to incorporate mature codes without adapting them. For the internal coupling method, the neutronics code and T/H code are integrated based on a same framework as two separate modules, where the coupling parameters are transferred in memory. There are two advantages of this approach. Firstly, efficiency can be enhanced by exchanging data in memory instead of external files because the latter one needs frequent and a huge amount of I/O operations. Secondly, the two modules can share the geometry information, making the spatial mapping much easier. Therefore, the internal coupling method is adopted to couple NECP-X with SUBSC.

6.2. Spatial mapping

Currently, the following thermal-hydraulics parameters of each pin cell are used to update the cross sections for the neutronics calculation: average fuel temperature, average cladding temperature, average temperature and density of coolant surrounding the rod. Since resonance absorption generally takes place on the surface of a resonance lump, the effective temperature of fuel pellet is used to assume more importance of the surface region than the center region. In this paper, the Arnold and Dannels’s model is chosen to calculate the effective temperature 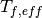${T_{f,eff}}$ .

${T_{f,eff}} = {T_s} + 0.35\left( {{T_c} - {T_s}} \right)$

Where

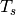
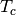
${T_s}$ is surface temperature and ${T_c}$ is the centerline temperature.

Due to the difference of solution meshes, appropriate spatial mapping between NECP-X and SUBSC is important. Figure shows the radial spatial mapping approach for the NECP-X/SUBSC coupling. Specifically, for the coolant part, volume-weighted density and mass-weighted temperature of four channels (SUBSC index: 25, 26, 35, 36) are used to update (NECP-X index: 15) the coolant cross sections for neutronics calculation.

Radial mesh mapping between NECP-X and SUBSC

Figure provides the axial spatial mapping. Due to the non-fuel structures, such as plenum, end plugs, nozzle and core plates, two approximations need to be made to accomplish the axial mesh mapping. On one hand, the average inlet conditions of the coolant at the bottom of the active fuel rod are utilized to approximate the T/H parameters of all the non-fuel structures below the active fuel, i.e. lower end plug, lower gap, bottom nozzle, lower core plate, lower reflector, etc. On the other hand, the average outlet conditions of the coolant at the top of the active fuel rod are used to approximate the T/H parameters of all the non-fuel structures above the active fuel, i.e. upper end plug, upper gap, top nozzle, upper core plate, upper reflector, etc.

Axial mesh mapping between NECP-X and SUBSC

6.3. An effective relaxation method

Since the computational burden is rather large for the high-fidelity coupling calculation, especially the full core coupling calculation. A relaxation method was implemented with the goal of speeding up the convergence behavior.

The traditional relaxation method [8] consists in weighting the results of the actual simulation step with the ones of the previous step by applying relaxation factor x. Take the fuel temperature as an example, the actual temperature is obtained as follows:

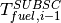$T_{f,i}^{weighted} = \left( {1 - x} \right) \cdot T_{fuel,i - 1}^{SUBSC} + x \cdot T_{fuel,i}^{SUBSC}$

Where

$T_{fuel,i - 1}^{SUBSC}$ is the fuel temperature from the T/H code of the previous step.

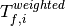$T_{f,i}^{weighted}$ is for the neutronics calculation of the current step,

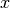is the relaxation factor whose value is recommended to be 0.5.

In this paper, a new relaxation method is proposed by weighting the results of two “relaxed” ones of current and previous steps, since the “relaxed” one is newer. The actual temperature can be obtained as follows:

$T_{f,i}^{weighted} = \left( {1 - x} \right) \cdot T_{f,i - 1}^{weighted} + x \cdot T_{fuel,i}^{SUBSC}$

If we set x to be 0.5, equation (2) can be rewritten in a recursion form as:

$T_{f,n}^{weighted} = {0.5^1} \cdot T_{fuel,n}^{actual} + {0.5^2} \cdot T_{fuel,n - 1}^{SUBSC} + ...... + {0.5^{n - 1}} \cdot T_{fuel,2}^{SUBSC} + {0.5^{n - 1}} \cdot T_{fuel,1}^{SUBSC}$

The new relaxation method considers contributions from the current step combined with all previous steps. Both the traditional and new relaxation methods were implemented in the NECP-X/SUBSC coupling code.

【Close Window】